1.OpenAPI可能面临的问题
- 信息保密问题:网络报文中的信息可能会泄露,例如身份证等信息 - 加密
- 信息篡改问题:网络报文被篡改,例如转账接受人 - 签名
- 通信对象认证问题:和你通信的人可能是被劫持的对象 - 签名
2.加密:对称加密 / 非对称加密
2.0.什么是加密
注意加密也一定需要能解密出来。
组成:一般密码系统通常由 明文 + 密钥 + 算法组成,明文 + 密钥是原材料,算法是配方,结果就是产出密文
密码算法要考虑的关键因素是让破解者难以通过明文、密文、以及其他信息推断出密钥或者缩小密钥的范围,从而暴力破解出密钥
2.1.对称加密
对称密码指加密和解密使用同样的密钥,就是加密方和解密方都要持有同样的密钥,性能高
由于对称加密需要双方持有同一密钥,因此就会引发出如何确定同一密钥,也就是密钥配送问题,如何协商出一致的秘钥
解决方案:
2.2.非对称加密
非对称密码指加密和解密使用不同密钥。
非对称加密需要4个密钥。通信双方各自准备一对公钥和私钥。其中公钥是公开的,由信息接受方提供给信息发送方。公钥用来对信息加密。私钥由信息接受方保留,用来解密。既然公钥是公开的,就不存在保密问题。也就是说非对称加密完全不存在密钥配送问题!你看,是不是完美解决了密钥配送问题?
但是,非对称加密过程容易产生中间人问题,中间人攻击指的是在通信双方的通道上,混入攻击者。他对接收方伪装成发送者,对放送放伪装成接收者。
他监听到双方发送公钥时,偷偷将消息篡改,发送自己的公钥给双方。然后自己则保存下来双方的公钥。
如此操作后,双方加密使用的都是攻击者的公钥,那么后面所有的通信,攻击者都可以在拦截后进行解密,并且篡改信息内容再用接收方公钥加密。而接收方拿到的将会是篡改后的信息。实际上,发送和接收方都是在和中间人通信
和对称加密相比较,非对称加密有如下特点:
1、非对称加密解决了密码配送问题
2、非对称加密的处理速度只有对称加密的几百分之一。不适合对很长的消息做加密。
2.2.1.如何解决公钥的传输解决中间人问题 - 证书解决
那么实际在通信双边的公钥传输过程中,如何明确拿到的公钥就是正确的呢,因此我们是不是就需要验证对端的身份合法?因此引出了证书
2.3.证书
证书是能够证明你身份的文件,类似于身份证,证书包括如下几个部分:
- 身份证姓名:对应证书的公钥所有者
- 身份证号:通信方公钥
- 身份证签发机关:证书颁发者
- 身份证有效期限:证书有效期
- 身份证防伪条纹:认证机构对公钥的签名
工作机制
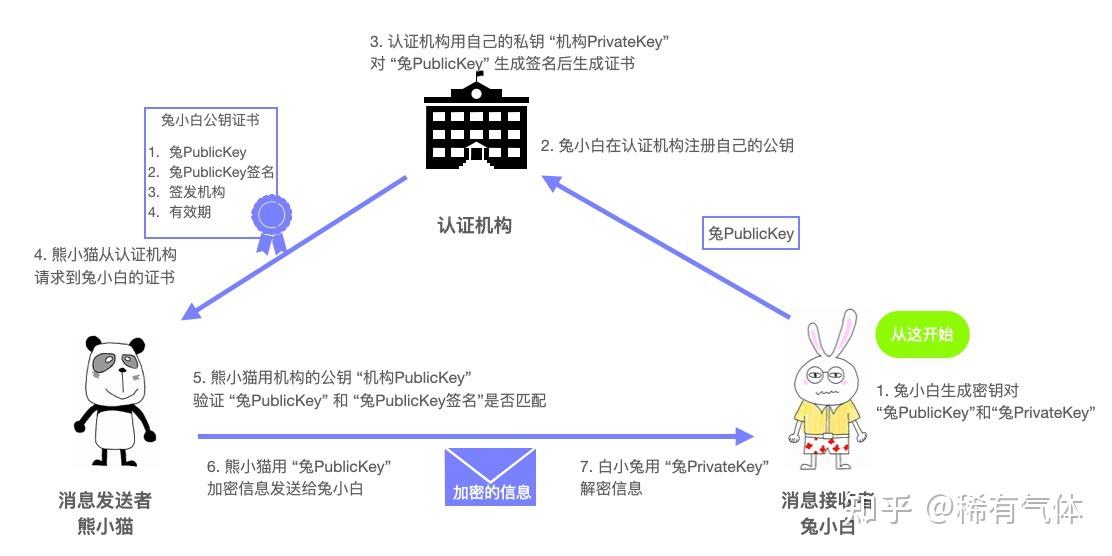
大致流程可以概述为:
- 对端在认证机构(CA)注册自己的公钥
- CA使用自己的机构私钥对证书进行签名,生成证书
- 接收端使用CA的公钥对证书进行验签
其中又会涉及到机构的合法性,此时又会引入证书链,也就是有更高级的证书机构对证书机构进行背书,最终会到根CA
3.签名
我们通过加密来保障了内容的隐私性,那假设我们发出去的报文被劫持方劫持并篡改,再使用公钥进行发送,此时会发生篡改的问题。接收人是无法识别的。这里就需要使用电子签名来保证信息的完整性(来源方正确+信息没有被篡改,例如我能知道我收到的这个信息是肯德基、麦当劳商户发起的)
如何确保来源方正确:对端用自己的私钥加签,服务端用对端的公钥进行签名的验证,如果能通过则验证对端是来源合法。(当然此时也会出现中间人问题,一样用证书解决)
如何确保报文没有被篡改:当然我们可以直接对原报文进行加密生成签名,但是由于考虑到性能,我们基于报文生成一个较短的单向散列函数值,并基于单向散列值进行签名的生成,由于散列函数存在同样的报文生成的散列函数唯一的特性,因此其实散列函数就能代表一段报文。
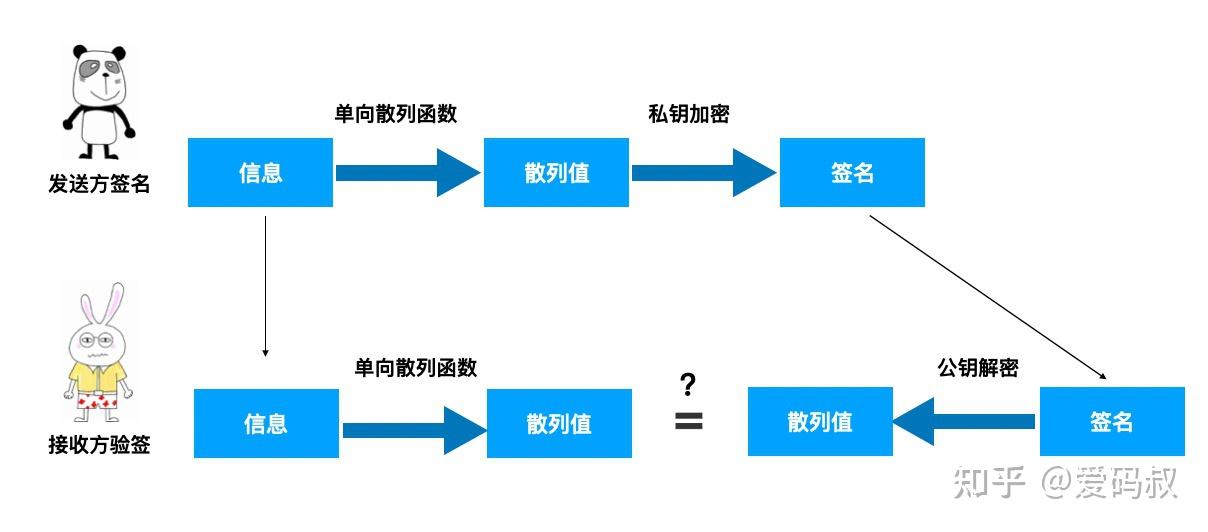
散列函数:
- 计算出的散列值是固定的,并且短。
- 不同的消息,散列值不同。
- 计算的速度要快。信息很长的时候,也要保证快速计算。