• 1.分治任务模型
• 2.Fork/Join的使用

Java并发包提供了一种叫做Fork/Join的并行计算框架，用来支持分治这种模型。

分治思想在很多领域都有广泛的应用，例如算法领域有分治算法（归并排序、快速排序都属于分治算法，二分法查找也是一种分治算法）；大数据领域知名的计算框架 MapReduce 背后的思想也是分治

1.分治任务模型

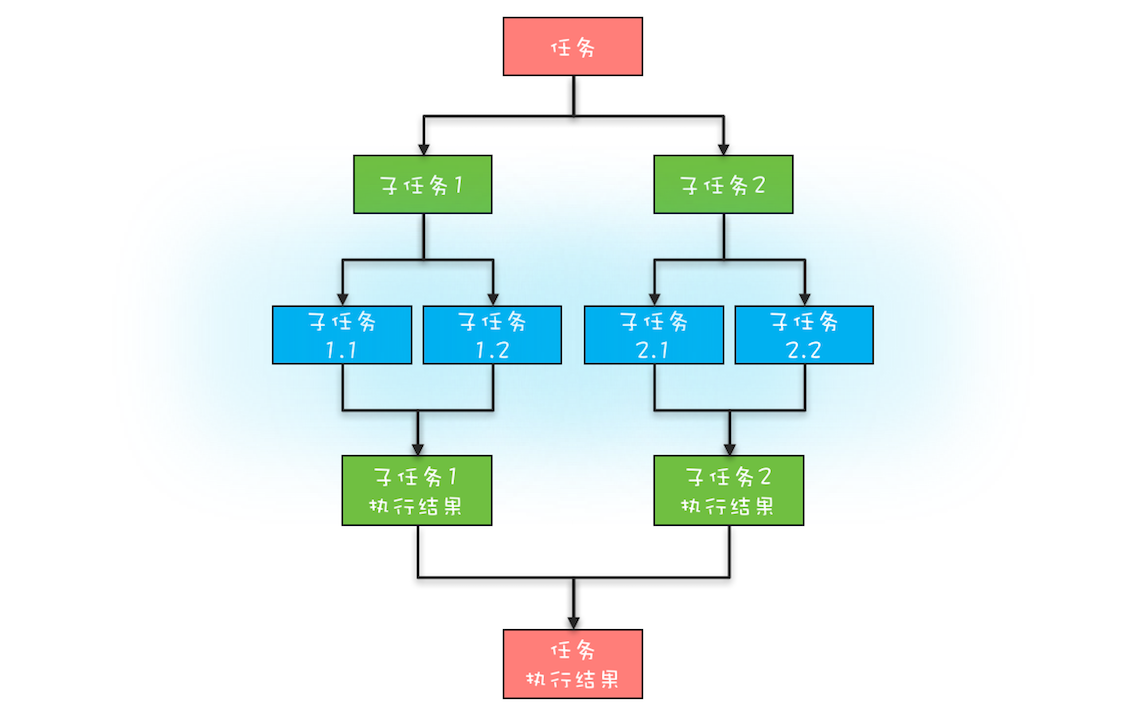
分治模型可以划分为如下两个阶段：

1. 任务分解：将任务迭代的分解为子任务，直至子任务可以计算出结果
2. 结果合并：逐层合并子任务的执行结果，直至获得最终结果

2.Fork/Join的使用

Fork对应的是分治任务模型中的任务分解，Join对应的是结果合并。

Fork/Join 计算框架主要包含两部分，这两部分有点类似于ThreadExecutorPool和Runnable的关系，可以理解为将任务提交到线程池去执行：

1. 分治任务的线程池ForkJoinPool
2. 分治任务ForkJoinTask，其是一个抽象类，ForkJoinTask 有两个子类——RecursiveAction 和 RecursiveTask，通过名字你就应该能知道，它们都是用递归的方式来处理分治任务的。这两个子类都定义了抽象方法 compute()，不过区别是 RecursiveAction 定义的 compute() 没有返回值，而 RecursiveTask 定义的 compute() 方法是有返回值的。这两个子类也是抽象类，在使用的时候，需要你定义子类去扩展。

解决斐波那契数列的实例代码如下：

static void main(String[] args){
  // 创建分治任务线程池  
  ForkJoinPool fjp = 
    new ForkJoinPool(4);
  // 创建分治任务
  Fibonacci fib = 
    new Fibonacci(30);   
  // 启动分治任务  
  Integer result = 
    fjp.invoke(fib);
  // 输出结果  
  System.out.println(result);
}
// 递归任务
static class Fibonacci extends 
    RecursiveTask<Integer>{
  final int n;
  Fibonacci(int n){this.n = n;}
  protected Integer compute(){
    if (n <= 1)
      return n;
    Fibonacci f1 = 
      new Fibonacci(n - 1);
    // 创建子任务  
    f1.fork();
    Fibonacci f2 = 
      new Fibonacci(n - 2);
    // 等待子任务结果，并合并结果  
    return f2.compute() + f1.join();
  }
}